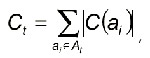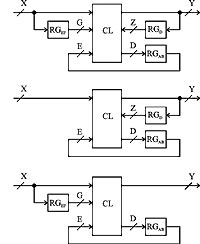
В. Соловьев, А. Климович

Синтез на ПЛИС совмещенных моделей конечных автоматов

Рассматривается новый подход к проектированию конечных автоматов на ПЛИС, когда в рамках одной структурной модели, названной совмещенной, объединяется несколько различных моделей конечных автоматов. Это позволяет наиболее полно использовать архитектурные возможности ПЛИС и положительные качества каждой модели для реализации конечных автоматов. Экспериментальные исследования показали, что применение метода синтеза совмещ╦нных моделей, по сравнению с методами пакетов MAX+PLUSII фирмы Altera и WebPack фирмы Xilinx, позволяет снизить стоимость реализации, в среднем, в 2√3,5 раза, а для отдельных примеров ≈ в 9 раз, а также повысить быстродействие, в среднем, в 2 раза, а для отдельных примеров ≈ в 6 раз.

Введение

В предыдущих статьях данной серии были рассмотрены оригинальные структуры конечных автоматов, позволяющие использовать триггеры выходных макроячеек ПЛИС [1] (автоматы классов C и D) и входных буферов ПЛИС [2] (автоматы классов E и F) в качестве элементов памяти конечных автоматов. Автоматы классов C-F показали высокую эффективность как по стоимости реализации, так и по быстродействию. Однако на практике конечные автоматы классов C-F в "чистом" виде встречаются редко. Обычно синтезируемый конечный автомат частично обладает свойствами сразу нескольких классов автоматов C-F. Поэтому возникает необходимость совмещения в рамках одной модели нескольких классов автоматов с тем, чтобы максимально использовать положительные качества каждого класса C-F, а также архитектурные возможности ПЛИС для реализации конечных автоматов.

Совмещать в одной структуре несколько моделей различных классов конечных автоматов можно только в случае совпадения временных параметров выходных сигналов каждой модели. В противном случае, может сложиться ситуация, когда значения выходных сигналов, формируемых в одном и том же состоянии конечного автомата, на выходе схемы будут появляться в различных тактах автоматного времени. Из анализа временного функционирования автоматов классов A-F [3] следует, что допустимы следующие четыре совмещ╦нные модели конечных автоматов: ADE, AD, AE и BF. На основании этих четыр╦х совмещ╦нных моделей пут╦м установки регистров на входы и/или выходы, а также защ╦лок на входы, можно построить ещ╦ 20 совмещ╦нных моделей конечных автоматов, допускающих эффективную реализацию на ПЛИС.

Структуры совмещенных моделей конечных автоматов

Структуры совмещ╦нных моделей показаны на рис. 1. Здесь комбинационная схема CL реализует выходные функции и функции возбуждения элементов памяти; регистр RGEF служит для хранения кодов состояний, определяемых входными наборами (автоматы классов E и F); регистр RGD - для хранения кодов состояний, определяемых выходными наборами (автомат класса D), и регистр RGAB - для хранения кодов состояний автоматов классов A и B. В совмещ╦нных моделях содержимое входного регистра RGEF определяется значениями входных переменных множества X = {x₁,...,x_L}, содержимое выходного регистра RGD определяется значениями выходных переменных множества Y = {y₁,...,y_N} и содержимое внутреннего регистра RGAB определяется значениями функций переходов множества D = {d₁,...,d_R}. Коды внутренних состояний конечного автомата определяются значениями переменных множеств G = = {g₁,...,g_L}, Z = {z₁,...,z_N} и E = {e₁,...,e_R}, формируемых на выходах регистров RG_EF, RG_D и RG_AB, соответственно.

Рисунок 1. Структуры совмещенных моделей конечных автоматов: ADE (а), AD (б), AE и BF (в)

Отметим, что в совмещ╦нных моделях конечных автоматов регистр RGEF реализуется входными буферами, регистр RG_D - выходными макроячейками, а регистр RG_AB - скрытыми макроячейками ПЛИС.

Кодирование внутренних состояний совмещенных моделей конечных автоматов

Вначале рассмотрим кодирование внутренних состояний конечных автоматов для совмещ╦нной модели ADE, а затем уточним этот метод для моделей AD, AE и BF.

Суть кодирования заключается в том, чтобы сделать все внутренние состояния различимыми между собой, то есть все коды внутренних состояний конечного автомата должны быть взаимно ортогональны. Входные и выходные наборы конечного автомата, определяемые значениями переменных множеств G = {g₁,...,g_L} и Z = {z₁,...,z_N}, частично решают эту задачу. Дальнейшее решение заключается во введении минимального числа R дополнительных переменных e₁,...,e_R множества E и кодировании отдельных групп состояний двоичными кодами.

Пусть, как и прежде [1,2], конечный автомат задан таблицей переходов, столбцы которой имеют обозначения a_m, a_ы, X(a_m,a_ы) и Y(a_m,a_ы). Для решения задачи кодирования внутренних состояний совмещ╦нной модели ADE строится троичная матрица W. Строки матрицы соответствуют внутренним состояниям конечного автомата, а столбцы - переменным множеств G и Z. На пересечении строки, соответствующей некоторому состоянию a_i, a_i € A, и столбца, соответствующего переменной g_j, g_j € G, ставится единица, если входная переменная x_j входит в условие X(a_i) в прямом значении, ноль - в инверсном, и неопредел╦нное значение (дефис), если переменная x_j не входит в условие X(a_i), где X(a_i) - условие перехода в состояние a_i. Значение X(a_i) определяется следующим образом: если все переходы в состояние a_i, a_i € A, осуществляются под воздействием одного и того же входного набора X(a_m,a_i), то полагается X(a_i) := := X(a_m,a_i), иначе полагается X(a_i) := пустое множество. На пересечении строк, соответствующих состоянию a_i, a_i € A, и столбца, соответствующего переменной z_j, z_j € Z, ставится единица, если y_j € Y(a_i), и ноль в противном случае, где Y(a_i) - подмножество выходных переменных, принимающих единичные значения на переходах в состояние a_i. Значение Y(a_i) определяется следующим образом: если на всех переходах в состояние a_i, a_i € A, формируется один и тот же выходной набор Y(a_m,a_i), то полагается Y(a_i) := Y(a_m,a_i), иначе полагается Y(a_i) := пустое множество. Теперь задачу кодирова ния внутренних состояний совмещенной модели конечного автомата можно сформулировать следующим образом.

Задача 1. Ввести минимальное число R дополнительных переменных e1,...,eR и закодировать строки матрицы W таким образом, чтобы все строки матрицы W были взаимно ортогональны.

Для решения задачи 1 строится граф H ортогональности строк матрицы W. Вершины графа H соответствуют строкам матрицы W (то есть внутренним состояниям конечного автомата). Две вершины i и j графа H соединяются ребром, если строки i и j матрицы W ортогональны между собой. Теперь задача 1 сводится к нахождению в графе H минимального числа T полных подграфов H₁,...,H_T, вершины которых не пересекаются, и приписывании этим подграфам двоичных кодов, определяемых значениями переменных e₁,...,e_R.

На основании вышеизложенного для решения задачи 1 может быть предложен следующий алгоритм.

Алгоритм 1

1. Строится граф H ортогональности строк матрицы W.
2. Из графа H удаляются вершины, связные со всеми другими вершинами графа (соответствующие им стоки матрицы W ортогональны всем другим строкам).
   Полагается t := 0.
3. Полагается t := t + 1. В графе H отыскивается максимальный полный подграф H_t.
4. Из графа H удаляются вершины подграфа H_t. Если множество вершин графа H пусто, то выполняется переход к пункту 5, иначе - к пункту 3.
5. Определяется число R дополнительных переменных e₁,...,e_R, R = intlog₂T, где T - число полных подграфов.
6. Для каждого подграфа H_t определяется цена C_t следующим образом:

   

   где A_t - множество внутренних состояний конечного автомата, соответствующих вершинам подграфа H_t, t = 1,T; C(a_i) - множество переходов, которые оканчиваются в состоянии a_i, a_i € A.

7. Каждому подграфу H_t, t = 1,T, ставится в соответствие двоичный код, определяемый значениями переменных e₁,...,e_R, прич╦м коды с минимальным числом единиц в первую очередь приписываются подграфам, для которых C_t = min.
8. В матрицу W добавляются столбцы, соответствующие переменным e₁,...,e_R. Содержимое этих столбцов определяется кодами соответствующих подграфов.
9. Определяются коды внутренних состояний конечного автомата. Каждый код K(a_i) внутреннего состояния a_i, a_i € A, определяется содержимым строки i матрицы W. Если на пересечении строки i и столбца j находится единица, то переменная, соответствующая столбцу j, входит в код K(a_i) состояния a_i в прямом значении, ноль - в инверсном, дефис - переменная не входит в код K(a_i) состояния a_i.
10. Конец.

Рассмотренный метод без всяких изменений может быть примен╦н при кодировании внутренних состояний конечных автоматов моделей AE и BF. При кодировании внутренних состояний конечных автоматов совмещ╦нной модели AD троичная матрица W будет содержать столбцы, соответствующие только переменным множества Е.

Метод синтеза совмещенных моделей конечных автоматов

Метод синтеза совмещ╦нных моделей конечных автоматов рассмотрим на примере модели ADE, а затем уточним этот метод для моделей AD, AE и BF. Использование совмещенной модели автоматов преследует две основные цели:

• минимизацию числа R дополнительных элементов памяти;
• упрощение функций переходов и выходов, то есть упрощение комбинационной части конечного автомата.

Обе цели достигаются пут╦м широкого использования моделей автоматов классов D и E, а также операции расщепления состояний. В предлагаемом ниже алгоритме синтеза расщепление состояний прекращается, как только это приводит к увеличению значения R, а в качестве окончательного принимается решение, которое последний раз вызвало уменьшение R.

Пусть A - множество всех внутренних состояний конечного автомата. Определим множество AE, AE Н A, состояний автомата класса E, то есть множество состояний, коды которых определяются входными наборами. Обозначим через U(a_i) множество всех условий переходов в состояние a_i, a_i € A:

U(a_i) = {X(a_m,a_i) | a_m € B(a_i)}, (1)

где B(a_i) - множество состояний, переходы из которых оканчиваются в состоянии a_i.

Состояние a_i, a_i € A, является состоянием автомата класса E, то есть a_i € AE, если выполняются условия:

|U(a_i)| = 1 и (2)
U(a_i) U(a_j) = пустое множество (3)
при i j для всех a_j € A.

Выполнение (2) обеспечивает, что все переходы в состояние ai осуществляются по одному и тому же условию перехода, а выполнение (3) обеспечивает, что условия переходов в состояние ai не вызывают переходов в другие состояния автомата.

Удовлетворение условиям (2) выполняется пут╦м расщепления состояний. Удовлетворение условиям (3) осуществляется пут╦м введения дополнительных переменных обратных связей и соответствующих им элементов памяти для различия кодов внутренних состояний автомата.

Пусть U_E(a_i) - множество условий переходов в состояние a_i, a_i € A, которые не встречаются на переходах в другие состояния, то есть для которых выполняется условие (3), U_E(a_i) U(a_i). Обозначим через A*_E множество состояний, для которых нарушено условие (2), то есть множество состояний, которые можно расщеплять с целью получения состояний автомата класса E.

Пусть V(a_i) - множество наборов выходных переменных, формируемых на переходах в состояние a_i, a_i € A:

V(a_i) = {Y(a_m,a_i) | a_m € B(a_i)}. (4)

Состояние a_i, a_i € A, является состоянием автомата класса D, то есть a_i € A_D, если выполняются условия:

|V(a_i)| = 1 и (5)
V(a_i) V(a_j) = пустое множество (6)
при i j для всех a_j € A.

Выполнение условия (5) обеспечивает, что на всех переходах в состояние a_i формируется один и тот же выходной набор, а выполнение (6) обеспечивает, что выходной набор V(a_i) не встречается на переходах в другие состояния конечного автомата.

Пусть V_D(a_i) - множество наборов выходных переменных, формируемых на переходах в состояние a_i, a_i € A, которые не встречаются на переходах в другие состояния, то есть V_D(a_i) - подмножество множества V(a_i), V_D(a_i) V(a_i), для которого выполняется условие (6). Пусть также A*_D - множество состояний, для которых нарушено условие (5), то есть множество состояний, которые можно расщеплять с целью получения состояний автомата класса D.

Определим стоимость S(a_i) расщепления состояния a_i как число строк, на которое увеличивается таблица переходов в результате расщепления состояния a_i, a_i € A*_D A*_E:

S(a_i) = |V(a_i) √ 1|·|P(a_i)|, если a_i € A*,_D, (7)
S(a_i) = |U(a_i) √ 1|·|P(a_i)|, если a_i € A*_E,

где P(a_i) - множество переходов из состояния a_i. В процессе синтеза конкретное значение S(a_i) выбирается в зависимости от того, каким образом производится расщепление: по выходным (a_i € A*_D) или по входным (a_i € A*_E) наборам.

На основании вышеизложенного, обобщ╦нный алгоритм синтеза совмещенной модели конечных автоматов ADE можно представить следующим образом.

Алгоритм 2

1. Полагается R* := 1000.
2. Строится матрица кодирования внутренних состояний W, решается задача 1, определяется значение R.
3. Если R > R*, то выполняется переход к пункту 7. Иначе, если R < R*, то полагается R* := R и запоминаются результаты синтеза (таблица переходов и коды состояний).
4. Определяются множества V(a_i), V_D(a_i), U(a_i) и U_E(a_i), a_i € A, а также множества A*_D и A*_E. Если A*_D И A*_E = пустое множество,то выполняется переход к пункту 7, иначе - к пункту 5.
5. Для всех состояний a_i, a_i € A*_D A*_E, определяется цена H(a_i), H(a_i) = max(|V_D(a_i)|, |U_E(a_i)|), эффективности использования автоматов классов D или E в случае расщепления состояния a_i. Для расщепления выбирается состояние a_i, a_i € A*_D A*E, по следующим критериям: 1) H(a_i) = max, 2) S(a_i) = min. Первый критерий обеспечивает наибольшую эффективность использования автоматов классов D или E, а второй - минимальное увеличение строк таблицы переходов.
6. Выполняется расщепление состояния a_i, выбранного в пункте 5. Если |V_D(a_i)| |U_E(a_i)|, то расщепление производится во выходным наборам множества V(a_i), иначе - по входным наборам множества U(a_i).
   Выполняется переход к пункту 2.
7. В качестве результата синтеза принимается решение, запомненное в пункте 3.
8. Строится структурная таблица переходов конечного автомата, определяются логические уравнения реализуемых функций.
9. Конец.

Отметим, что в начале выполнения алгоритма 2 значение R* принимается заведомо большим, чем необходимо, поэтому в пункте 3 по крайней мере один раз выполнится запоминание результатов синтеза.

Пример. Рассмотрим работу алгоритма 2 на примере синтеза совмещ╦нной модели конечного автомата Мили, таблица переходов которого приведена в табл. 1. Решение задачи 1 приводит к определению значения R* = 2. Множества V(a_i), V_D(a_i), U(a_i) и U_E(a_i) для данного примера приведены в табл. 2, на основании которых определяются следующие множества: A_D = {a₄}; A*_D = {a₃,a₅}; A_E = {a₁,a₂,a₃} и A*_E = {a₄,a₅}. Для расщепления выбирается состояние a₅, поскольку |V_D(a₅)| = |U_E(a₅)| = max = 3. Результаты расщепления состояния a₅ по выходным наборам множества V(a₅) приведены в табл. 3. Матрица W, построенная для решения задачи 1, приведена в табл. 4 (первые восемь столбцов). Граф H ортогональности строк матрицы W показан на рис. 2.

Таблица 1. Таблица переходов исходного конечного автомата

Таблица 2. Множества V(a_i), VD(a_i), U(a_i) и UE(a_i)

Таблица 3. Таблица переходов после расщепления состояния a₅

Таблица 4. Матрица W для кодирования внутренних состояний

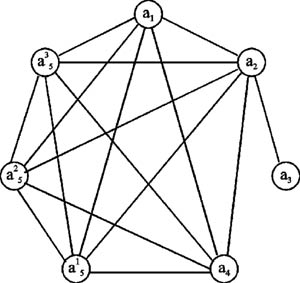
Рисунок 2. Граф H ортогональности строк матрицы W

Вначале из графа H удаляется вершина a₂, связанная со всеми остальными вершинами графа. Затем в графе H последовательно выделяются два полных подграфа H₁ и H₂, для которых A₁ = {a₁, a₄, a₅¹, a₅², a₅³} и A₂ = {a₃}. Поскольку два подграфа можно закодировать одной двоичной переменной, то имеем R = 1. Дальнейшее расщепление состояний не приводит к уменьшению R, поэтому полученное решение принимается за окончательное. В матрицу W добавляется один столбец, соответствующий дополнительной переменной e₁. Строки таблицы W, соответствующие подграфу H₁, кодируются нулевым значением переменной e₁, а подграфу H₂ - единичным. На основании содержимого строк матрицы W определяются следующие значения кодов внутренних состояний автомата:

K(a₁) = ¯g₄╥¯z₁╥¯z₂╥¯z₃╥¯z₄╥¯e₁;
K(a₂) = g₁╥¯z₁╥¯z₂╥z₃╥z₄;
K(a₃) = ¯g₁╥e₁;
K(a₄) = ¯z₁╥¯z₂╥z₃╥¯z₄╥¯e₁;
K(a_5¹) = ¯z₁╥¯z₂╥¯z₃╥z₄╥¯e₁;
K(a₅²) = g₄╥¯z₁╥z₂╥¯z₃╥¯z₄╥¯e₁;
K(a₅³) = g₄╥z₁╥¯z₂╥¯z₃╥¯z₄╥¯e₁.

Структурная таблица переходов представлена в табл. 5, на основании которой составляются следующие логические уравнения реализуемых функций:

d₁ = ¯g₄╥¯z₁╥¯z₂╥¯z₃╥¯z₄╥¯e₁╥¯x₁ + g₁╥¯z₁╥¯z₂╥¯z₃╥z₄╥¯x₁;
y₁ = ¯z₁╥¯z₂╥¯z₃╥z₄╥¯e₁╥x₄ + g₄╥¯z₁╥z₂╥¯z₃╥¯z₄╥¯e₁╥x₄ + + g₄╥z₁╥¯z₂╥¯z₃╥¯z₄╥¯e₁╥x₄;
y₂ = ¯z₁╥¯z₂╥z₃╥¯z₄╥¯e₁╥x₄;
y₃ = ¯g₄╥¯z₁╥¯z₂╥¯z₃╥¯z₄╥¯e₁ + g₁╥¯z₁╥¯z₂╥z₃╥z₄╥x₁╥¯x₂ + + ¯g₁╥e₁╥x₃;
y₄ = ¯g₄╥¯z₁╥¯z₂╥¯z₃╥¯z₄╥¯e₁ + g₁╥¯z₁╥­z₂╥z₃╥z₄╥x₁╥x₂ + + ¯g₁╥e₁╥¯x₃.

Таблица 5. Структурная таблица переходов

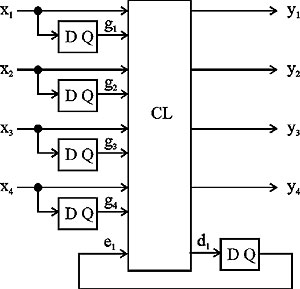
Окончательная реализация совмещ╦нной модели ADE показана на рис. 3.

Рисунок 3. Реализация совмещ╦нной модели ADE

Если для всех a_i, a_i € A, положить U(a_i) := пустое множество, то алгоритм 2 без всяких изменений может быть примен╦н для синтеза конечных автоматов совмещенной модели AD. Если для всех a_i, a_i € A, положить V(a_i) := пустое множество, то алгоритм 2 также без всяких изменений может быть примен╦н для синтеза совмещ╦нной модели AE.

Для автоматов типа Мура возможно построение только одной совмещ╦нной модели BF. Дело в том, что временные параметры выходных сигналов автомата класса C существенно отличаются от временных параметров выходных сигналов автоматов классов B и F [3]. Поэтому, в общем случае, автомат класса C нельзя совмещать в рамках одной модели с автоматами классов B и F.

Метод синтеза совмещ╦нной модели BF полностью совпадает с рассмотренным выше методом синтеза совмещ╦нной модели AE. Отличие заключается только в том, что вместо исходного автомата типа Мили рассматривается автомат типа Мура. Переход от автомата типа Мили к автомату типа Мура можно выполнить с помощью алгоритма 2 работы [2].

Результаты экспериментальных исследований метода синтеза совмещенных моделей конечных автоматов

Метод синтеза совмещ╦нных моделей реализован программно в пакете ZUBR. Эффективность метода сравнивалась с методами синтеза пакета MAX+PLUSII фирмы Altera для семейств MAX 9000 и FLEX 10K, а также методами синтеза пакета WebPack фирмы Xilinx для семейств XC 9500 и VIRTEX2. В качестве исходных данных использовались эталонные примеры конечных автоматов, разработанные в центре MCNC (Microelectronics Center of North Carolina) [4].

Результаты сравнения стоимости реализации конечных автоматов, синтезированных с помощью метода синтеза совмещ╦нных моделей и методов пакета MAX+PLUSII для семейств MAX 9000 и FLEX 10K представлены соответственно в табл. 6 и 7, где Name - имя эталонного примера; L, N, M и P - число входов, выходов, внутренних состояний и переходов конечного автомата, соответственно; C₁ - число используемых макроячеек ПЛИС при синтезе конечного автомата с помощью метода синтеза пакета MAX+PLUSII для семейства MAX 9000; C₂, C₃ и C₄ - число используемых макроячеек ПЛИС семейства MAX 9000 при синтезе конечного автомата с помощью метода синтеза совмещ╦нной модели ADE, AD и AE, соответственно; C₅, C₆, C₇ и C₈ - то же, но для семейства FLEX 10K.

Таблица 6. Сравнение метода синтеза совмещенных моделей конечных автоматов с методами пакета MAX+PULSII для семейства MAX 9000

Name	L	N	M	P	C1	C2	C1/C2	C3	C1/C3	C4	C1/C4
beecount	3	4	7	28	9	6	1,5	6	1	6	1
dk14	3	5	7	56	12	11	1,1	10	1,1	12	1
ex3	2	2	10	36	8	4	2	4	2	4	2
ex5	2	2	9	32	11	4	2,75	4	2,75	4	2,75
ex7	2	2	10	36	10	4	2,5	4	2,5	4	2,5
keyb	7	2	19	170	27	13	2,08	17	1,59	17	1,59
lion9	2	1	9	25	7	3	2,33	3	2,33	3	2,33
s1	8	6	20	107	48	11	4,36	9	5,33	48	1
s27	4	1	6	34	4	3	1,33	3	1,33	4	1,33
train11	2	1	11	25	7	2	3,5	3	2,33	3	2,33
train4	2	1	4	14	3	2	1,5	3	1	3	1
							24,95		23,26		18,83
mid							2,27		2,11		1,71

Таблица 7. Сравнение метода синтеза совмещенных моделей конечных автоматов с методами пакета MAX+PULSII для семейства FLEX 10K

Name	C5	C6	C5/C6	C7	C5/C7	C8	C5/C8
beecount	37	9	4,11	10	3,7	10	3,7
dk14	75	39	1,92	39	1,92	45	1,66
ex3	22	9	2,44	8	2,75	10	2,2
ex5	23	8	2,88	4	5,75	6	3,83
ex7	20	4	5	4	5	4	5
keyb	102	72	1,42	1,04	1,04	83	1,23
lion9	23	5	4,6	3	7,66	3	7,66
s1	128	35	3,66	33	3,88	128	1
s27	40	9	4,44	9	4,44	20	2
train11	24	6	4	6	4	3	8
train4	6	4	1,5	4	1,5	3	2
			35,97		41,64		38,28
mid			3,27		3,79		3,48

Анализ табл. 6 и 7 показывает, что использование совмещ╦нных моделей конечных автоматов и соответствующих методов синтеза позволяет уменьшить число задействуемых макроячеек ПЛИС, в среднем, в 1,71√3,79 раза, а для отдельных примеров - в 8 раз.

В табл. 8 приведены результаты сравнения быстродействия синтезированных конечных автоматов для моделей AD и AE, где D₁ - максимальная задержка в наносекундах прохождения сигналов со входа на выход схемы при использовании пакета WebPack для семейства XC 9500; D₂ и D₃ - то же, но при использовании метода синтеза совмещ╦нных моделей AD и AE, соответ ственно. Анализ табл. 8 показывает, что метод синтеза совмещ╦нных моделей позволяет повысить быстродействие конечных автоматов, в среднем, в 2,14 раза, а для отдельных примеров - почти в 6 раз.

Таблица 8. Сравнение быстродействия конечных автоматов для семейства XC 9500

Name	D1	D2	D1/C2	C3	C1/C3
beecount	23,9	5	4,78	5	4,78
dk14	22,6	18,6	1,22	24,1	0,94
ex3	24	11,8	2,03	8,4	2,86
ex5	15,8	11,8	1,34	18,6	0,85
ex7	15,8	8,4	1,88	8,4	1,88
keyb	24,7	20	1,24	20	1,24
lion9	11	5	2,2	5	2,2
s1	20,6	26,8	0,77	29,9	0,69
s27	10,3	8,4	1,23	18,6	0,55
train11	29,9	5	5,98	5	5,98
train4	7,1	8,4	0,85	8,4	0,85
			23,52		22,82
mid			2,14		2,07

Литература

1. Соловьев В.В. Использование выходных макроячеек ПЛИС в качестве элементов памяти конечных автоматов // Chip News. 2003. ╧ 1. С. 17√23.
2. Соловьев В.В., Климович А. Использование входных буферов ПЛИС в качестве элементов памяти конечных автоматов // Chip News. 2003. ╧ 2. С. 30√34.
3. Соловьев В.В. Структурные модели конечных автоматов при их реализации на ПЛИС // Chip News. 2002. ╧ 9. С. 4√14.
4. Yang S. Logic synthesis and optimization benchmarks user guide. Version 3.0. Technical Report, Microelectronics Centre of North Carolina, 1991. 43 p.