|
В. Поляков Схемотехническое моделирование нелинейных резистивных инерционных нагрузокСхемотехническое моделирование является наиболее эффективным способом исследования проектируемого объекта на стадии формирования его принципиальной электрической схемы. Особое место занимает моделирование нагрузки создаваемых электронных преобразователей. Имеется целый ряд нагрузок, которые при включении в электрическую цепь проявляют свойства нелинейного инерционного резистора. К таким объектам относятся, например, приборы (установки), использующие различные виды электрического разряда, в частности, разрядные лампы. Сложность моделирования нагрузок, проявляющих свойства нелинейного инерционного резистора, заключается в том, что электрическую схему замещения таких нагрузок невозможно отобразить только совокупностью имеющихся в наборе пассивных и активных линейных элементов. Для создания их математической и схемотехнической моделей требуется математическое описание объекта, адекватно отражающее его электрические свойства и знание экспериментальных аппроксимирующих зависимостей для его параметров. Моделируемый объект при включении в электрическую цепь представляется как двухполюсник. Искомое дифференциальное уравнение, описывающее его поведение, может быть получено на основе уравнения баланса энергии dW/dt = P - Pп, (1) где dW/dt - скорость изменения внутренней энергии объекта; P - мгновенное значение потребляемой от источника питания мощности; Pп - текущие потери мощности (например, в виде излучения и тепла, теряемого при контакте с внешней средой). Выражение для потребляемой мощности можно записать как P = g╥uD², (2) где uD - текущее значение напряжения, g - электрическая проводимость. Мощность потерь определяется из условия dW/dt = 0 и может быть представлена следующей формулой Pп = P = gUD²(g), (3) где UD(g) - зависимость напряжения от проводимости в стационарных режимах. С уч╦том (2) и (3) запись уравнения (1) относительно проводимости имеет вид
где k1(g) = dW/dg ≈ коэффициент, учитывающий инерционные свойства. Нелинейное дифференциальное уравнение должно быть дополнено законом Ома iD = g╥uD (5) и зависимостями, определяющими температурный режим
TP = где iD - ток, T - текущая температура объекта, TP - равновесная температура объекта, TC - температура окружающей среды, Между температурой и электрическими свойствами объекта имеется однозначное взаимное соответствие, то есть T T Функции UD(g), k1(g), (7)√(9) и постоянная времени q определяются экспериментально и задаются в виде аппроксимирующих аналитических зависимостей. Обычно используется определ╦нный тип аппроксимирующего выражения и устанавливается функциональная зависимость между его коэффициентами и значениями текущей и равновесной температур. Таким образом, наличия уравнений (4)√(6) и аппроксимирующих зависимостей UD(g), k1(g) и (7)√(9) достаточно для создания математической и схемотехнической моделей. Далее более подробно косн╦мся вопросов создания схемотехнической модели. Базовым, то есть определяющим основную структуру модели, является уравнение (4). Решение этого уравнения относительно текущего значения напряжения с уч╦том (5) выглядит как
Вторым базовым является уравнение (6), запись которого в интегральной форме принимает вид
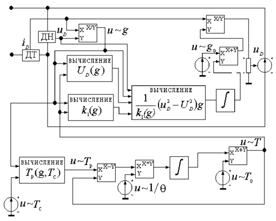
В формулах (10), (11): g0 и T0 начальные значения проводимости и температуры объекта, соответственно. Формула (10) отражает нелинейные свойства проводимости нагрузки, а также е╦ инерционные свойства, определяемые относительно быстрыми процессами е╦ изменения (например, процессами генерации и рекомбинации носителей заряда в плазме). Уравнение (11) отражает более медленные процессы, вызванные изменением температуры объекта. Модель, при необходимости, должна быть дополнена другими уравнениями, устанавливающими связь иных физических или химических процессов с электрическими параметрами нагрузки. Оста╦тся немного - перевести эту запись в некую совокупность взаимосвязанных между собой элементов, имеющихся в наборе какой-либо программы схемотехнического моделирования. Рисунок 1. Структурная схема модели
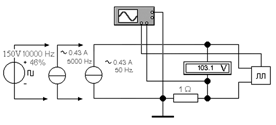
Структурная схема модели приведена на рис. 1 и представляет набор связанных между собой, согласно уравнениям (10) и (11), функциональных элементов: датчиков напряжения и тока, делителей, умножителей, сумматоров, интеграторов, управляемого источника напряжения и функциональных блоков для промежуточных расч╦тов и вычисления текущей и равновесной характеристик. Нагрузка представлена как источник напряжения, направление которого всегда противоположно направлению тока, а значение определяется упомянутыми функциональными зависимостями. Рисунок 2. Схема электропитания люминесцентной лампы
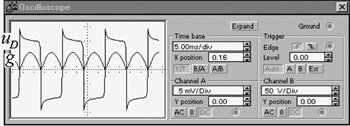
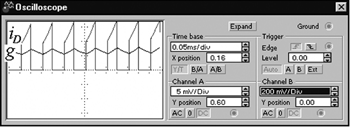
В качестве примера на рис. 2-5 представлены результаты моделирования люминесцентной лампы ЛБ40 с использованием популярной "Work-bench Pro". При моделировании параметров лампы использованы аналитическая аппроксимация вольт-амперной характеристики [1,2], а также результаты моделирования люминесцентных ламп, привед╦нные в [1]. Использовались линейные приближения зависимостей в области номинальной проводимости gном = IDном/UDном. Схема электропитания лампы приведена на рис. 2. Питание осуществлялось от источников синусоидального тока и импульсного напряжения. Электрическая схема модели (рис. 1) представлена в виде субблока "ЛЛ". Рисунок 3. Осциллограммы напряжения и проводимости лампы при питании от источника тока 50 Гц
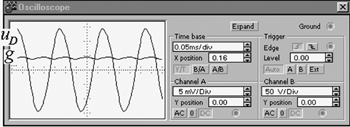
Рисунок 4. Осциллограммы напряжения и проводимости лампы при питании от источника тока 5000 Гц
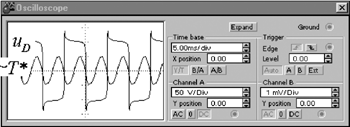
Рисунок 5. Осциллограммы напряжения и проводимости лампы при питании от источника импульсного напряжения
На рис. 3 и 4 приведены осциллограммы проводимости плазмы и напряжения на лам ри питании от источника синусоидального тока с частотой 50 и 5000 Гц, соответственно. На рис. 5 даны осциллограммы тех же параметров при питании от источника напряжения в виде прямоугольных импульсов, на рис. 6 - от источника тока частотой 50 Гц. Рисунок 6. Осциллограммы напряжения и относительной температуры лампы при питании от источника тока 50 Гц
Результаты моделирования, как минимум, качественно совпадают с известными результатами практических исследований динамических характеристик люминесцентных ламп [2]. Как видно из рис. 3, на промышленной частоте 50 Гц форма напряжения существенно нелинейная и близка к прямоугольной. Имеется пик напряжения при смене полярности тока (пик перезажигания). Проводимость плазмы в течение полупериода тока изменяется от практически нулевого значения в начале и конце и вала до максимального в середине. При питании током повышенной частоты (рис. 4) пульсации проводимости плазмы уменьшаются, текущее значение проводимости приближается к своему среднему значению. Форма напряжения становится практически синусоидальной и приближается к форме тока. Это объясняется тем, что при переходе на повышенную частоту плазма не успевает деионизироваться к моменту перезажигания. Концентрация электронов и, соответственно, проводимость практически не успевают измениться в течение полупериода. Измерение напряжения подтвердили известный факт, что на повышенной частоте действующее значение напряжения на разряде несколько ниже, чем при питании на частоте сети. Это явление объясняется тем, что при приближении формы напряжения к синусоидальной увеличивается коэффициент мощности лампы и, соответственно, уменьшается действующее значение напряжения, необходимого для достижения той же мощности. Наглядной иллюстрацией инерционных свойств разряда являются осциллограммы (рис. 5). На этапе действия импульса напряжения проводимость лампы резко возрастает примерно по экспоненциальному закону, а на этапе паузы ≈ уменьшается, стремясь к нулевому значению. Ток лампы скачкообразно возрастает до значения, определяемого амплитудой напряжения и текущим значением проводимости. Затем имеет место экспоненциальный рост тока до окончания действия импульса напряжения. Как показано в [1], при питании от импульсного источника напряжения разряд можно стабилизировать без применения индуктивного или емкостного балласта, если использовать быстродействующую систему регулирования. В квазиустановившемся режиме текущая температура практически неизменна вследствие своей инерционности. Е╦ колебания незначительны, однако они увеличиваются со снижением частоты питающего тока. Рис. 6 иллюстрирует относительное отклонение текущей температуры от е╦ среднего значения при питании от источника тока 50 Гц для тепловой постоянной Привед╦нные примеры наглядно демонстрируют возможности, открывающиеся при схемотехническом моделировании нелинейных инерционных нагрузок. Математическое описание и структура модели могут быть использованы при моделировании широкого спектра объектов, являющихся элементами электрической цепи: разряда, электролита, терморезисторов и других. Применение модели позволяет имитировать реальные процессы в системе "преобразователь √ нелинейная инерционная нагрузка" и учесть особенности нагрузки при решении вопросов управления электронным преобразователем, что значительно сокращает время разработки источника электропитания. Литература
|


 Схемотехническое моделирование нелинейных резистивных инерционных нагрузок
Схемотехническое моделирование нелинейных резистивных инерционных нагрузок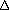 P ╥ RthO√C + TC = F(g,TC),
P ╥ RthO√C + TC = F(g,TC), 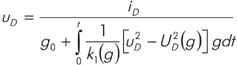 ,
,