В. Геппенер, А. Ланнэ, Д. Черниченко

    Часто оказывается, что wavelet-разложение сигнала по классической схеме не всегда оправдано. Это связано с тем, что сигнал раскладывается в сумму сигналов с шириной спектров, равной октаве, но для каждого конкретного сигнала такое разбиение не всегда является наилучшим. Мейер и Койфман предложили схему разложения сигнала по wavelet-пакету.

    На каждом уровне последующей фильтрации подвергается не только низкочастотная, но и высокочастотная составляющая. Общая схема фильтрации будет иметь вид двоичного дерева (рис. 1).

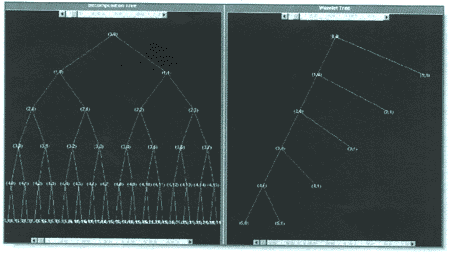
Рис. 1. Разложение по "стандартной" схеме (а) и по wavelet-пакету (б)

    Wavelet-пакетом является любой подграф G полного графа разложения, удовлетворяющий следующим свойствам:

• корень дерева принадлежит G;
• в каждой из вершин граф G либо делится на две части, либо прерывается.

    Сигнал, получающийся в каждом узле дерева wavelet-пакета можно интерпретировать как выход некоторого полосового фильтра. Сложность вычисления по полной схеме пропорциональна NlogN, где N является длиной сигнала.

    Для экономии вычислений и повышения качества разложения вводится аддитивная функция стоимости E( s), такая что E(0) = 0 и

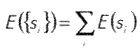
    где s_i - коэффициенты разложения в i-м узле дерева. 

    Далее, на основе введенной функции стоимости определяется наилучший подграф полного дерева.

    Если суммарная функция стоимости потомков узла меньше, чем функция стоимости предка, то они включаются в подграф, в противном случае, данный узел становится терминальным, то есть последующее разбиение этого узла не производится.

    Таким образом, можно адаптировать разложение к сигналу. Отметим, что такая адаптация не требует обучения или знания статистических свойств сигнала.

    Функции стоимости, используемые в GUI Wavemenu для определения наилучшего подграфа:

• Shannon - 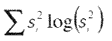, log(0) принимается равным 0;
• Threshold - число отсчетов, по абсолютному значению больших, чем заданный порог e;
• Norm - ;
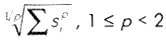• Log Energy - 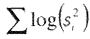, log(0) принимается равным 0;
• SURE - 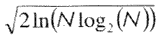, N - количество отсчетов;
• User - функция стоимости задается в MAT-файле.

    Для анализа и синтеза сигналов, используя разложение по wavelet-пакету, необходимо выбрать пункт "Wavelet Packet 1-D" в главном меню. Появится панель инструментов разложения одномерного сигнала по wavelet-пакету (рис. 2).

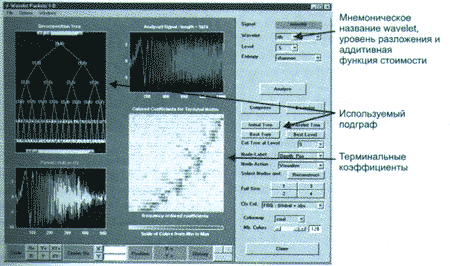
Рис. 2. Панель инструментов разложения одномерного сигнала по wavelet-пакету

Очистка сигнала от шумов

    Процедура фильтрации шума выглядит так же, как и при использовании стандартной схемы wavelet-преобразования, только модифицируются коэффициенты, находящиеся в терминальных узлах выбранного в соответствии с заданной функцией стоимости наилучшего подграфа полного дерева разложения.

    В качестве примера для демонстрации удаления шума будем использовать все тот же сигнал

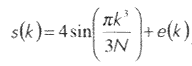
    находящийся в тестовом файле "noischir.mat" (его необходимо загрузить так же, как это делалось при использовании одномерного дискретного wavelet-преобразования).

    Произведем его разложение с использованием wavelet Добеши с 3-мя нулевыми моментами ('db3') до 5-го уровня, в качестве функции стоимости для поиска наилучшего подграфа будем использовать энтропию Шеннона (Shannon). Для разложения сигнала по wavelet-пакету нажмем кнопку "Analyze". Затем необходимо выбирать подграф, по которому будет производиться анализ и синтез сигнала.

    Подграфы полного дерева wavelet-пакета:

• Initial tree - полное бинарное дерево разложения;
• Wavelet tree - стандартная схема wavelet-преобразования;
• Best tree - выбирается лучшее дерево на основе заданной функции стоимости.

    Для вызова инструмента очистки сигнала от шума используется кнопка "De-noise", размещенная справа, под кнопкой "Analyze". Появится окно (рис. 3), в котором можно производить удаления шума из сигнала при разложении по wavelet-пакету.

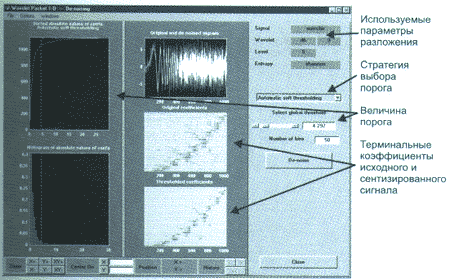
Рис. 3. Панель инструментов для очистки сигнала от шума при использовании разложения по wavelet-пакету

    Графики в левой части окна показывают гистограмму распределения wavelet-коэффициентов (внизу) и процент сохраненной энергии сигнала (вверху), в зависимости от выбранного порога (вертикальная пунктирная линия).

    При удалении шума из сигнала необходимо задать правило модификации терминальных коэффициентов выбранного подграфа, "hard' или "soft" (Automatic hard thresholding или Automatic soft thresholding, соответственно), и порог.

    При нажатии на кнопку "De-noise" происходит очистка сигнала от шума в соответствии с заданными параметрами. Очищенный от шума сигнал накладывается на исходный. Также выводятся графики wavelet-коэффициентов исходного и очищенного (синтезированного) сигнала.

Сжатие сигнала

    Схема сжатия сигнала при использовании разложения по wavelet-пакету такая же, как и при использовании стандартной схемы разложения: производится разложение исходного сигнала по wavelet-пакету, после чего запоминаются только те терминальные коэффициенты, которые больше заданного порога. Восстановление сигнала производится при помощи обратного преобразования, при этом пропущенные коэффициенты заменяются нулями.

    Как правило, при использовании разложения по wavelet-пакету получаются лучшие результаты сжатия сигнала, чем при использовании разложения по стандартной схеме.

    Для вызова инструмента сжатия сигнала при использовании разложения по wavelet-пакету (рис. 3) следует нажать кнопку "Compress", размещенную слева под кнопкой "Analyze".

    Например, при сжатии сигнала

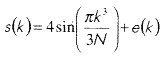
    используя разложение по wavelet-базису Добеши с 3-мя нулевыми моментами ('db3') и раскладывая сигнал до 5-го уровня с обнулением примерно 90% коэффициентов, мы получим следующие результаты.

    Используемые подграфы полного дерева разложения:

• полное бинарное дерево - 87,16% сохраненной энергии;
• лучшее дерево (используя в качестве функции стоимости энтропию Шеннона) - 87,54%;
• разложение по стандартной wavelet-схеме - 59,99%.

    Таким образом, при использовании разложения по wavelet-пакету при одинаковой степени сжатия мы получаем больший процент сохраненной энергии исходного сигнала, чем при использовании стандартной схемы; вычислительная сложность при этом увеличивается незначительно.

Использование непрерывного wavelet-преобразования

    Любой сигнал, обрабатываемый на компьютере, должен быть дискретным, то есть сигналом, который представлен измерениями в дискретные моменты времени. Непрерывное wavelet-преобразование (CWT) также работает в дискретном времени. Но, в отличие от дискретного преобразования, CWT оперирует с отсчетами, непрерывными по состоянию. Непрерывное wavelet-преобразование можно использовать как альтернативу кратковременному преобразованию Фурье с целью преодолеть сложности, связанные с разрешением по времени и частоте.

    Работу с непрерывным wavelet-преобразованием удобно продемонстрировать на примере. Выбираем пункт "Continuous Wavelet 1-D" в главном меню, после чего появится панель инструментов непрерывного wavelet-анализа для одномерного сигнала (рис. 4).

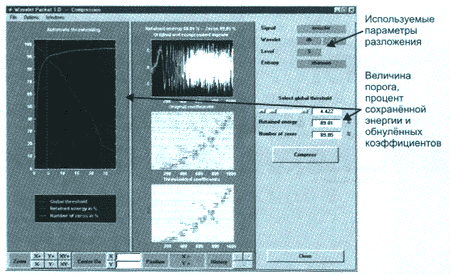
Рис. 4. Панель инструментов для сжатия сигнала при использовании разложения по wavelet-пакету

    В качестве примера будем использовать сигнал, содержащийся в тестовом файле mishmash.mat, который должен находиться в каталоге MATLAB toolbox/wavelet/wavedemo.

    Этот сигнал имеет следующий вид:

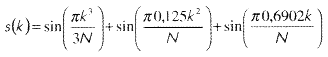
    где N - продолжительность сигнала, в нашем случае - 1024 отсчета; k = 1...N.

    Для загрузки сигнала выбираем пункт меню "File->Load signal". Когда появится диалог загрузки сигнала, выбираем тестовый MAT-файл mishmash.mat, который должен находиться в каталоге MATLAB toolbox/wavelet/wavedemo, нажав кнопку "OK".

    Наша задача - при помощи непрерывного wavelet-преобразования определить вид сигнала. Для начала произведем его анализ, используя wavelet Хаара в масштабах от 1 до 32. Для этого необходимо:

• выбрать тип wavelet ("haar") и уровни масштабирования 1-32 в верхнем правом углу утилиты;
• нажать кнопку "Analyze";
• после выполнения вычислений утилита отобразит график wavelet-коэффициентов (рис. 4). При этом можно задавать варианты представления вычисленных wavelet-коэффициентов: менять цветовую палитру и интенсивность цветов.

    Получившиеся wavelet-коэффициенты мало информативны; по ним нельзя точно сказать ни о виде сигнала, ни тем более получить какие-то численные оценки. Это связано с тем, что wavelet Хаара мало подходит для анализа сигналов подобного типа, так как очень плохо локализован в частотной области и имеет всего два нулевых момента. Для анализа рассматриваемого сигнала предпочтительнее wavelet Мейера, который имеет более подходящие характеристики.

    Результаты анализа сигнала с помощью wavelet Мейера представлены на рис. 5. Видно, что сигнал состоит из 3-х компонент. Здесь так же можно проследить, чем отличается разбиение частотно-временной полуплоскости wavelet-преобразования от кратковременного преобразования Фурье.

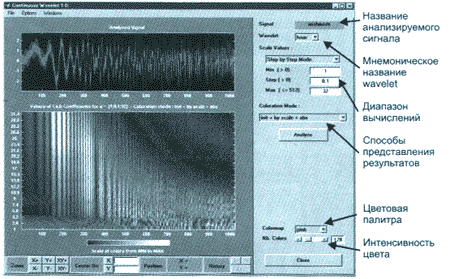
Рис. 5. Панель инструментов непрерывного wavelet-анализа одномерного сигнала

    Заметим, что если при помощи преобразования Фурье можно твердо определить наличие синусоиды только с постоянной частотой, то при помощи непрерывного wavelet-преобразования мы видим и можем оценить все компоненты исходного сигнала. Может показаться странным использование непрерывного wavelet-преобразования для анализа сигналов, где достаточно непросто правильно интерпретировать полученные результаты, если при кратковременном преобразовании Фурье можно получить исчерпывающую информацию. Следующий пример поможет почувствовать оправданность в определенных случаях применения wavelet-преобразования.

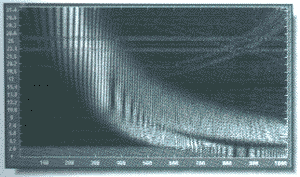
Рис. 6. Абсолютное значение wavelet-коэффициентов, полученных при анализе сигнала с помощью wavelet Мейера

    Допустим в некоторый момент времени на наш исходный сигнал наложился некоторый выброс. То есть сигнал теперь имеет следующий вид:

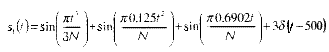
    Теперь наша задача - не только определить вид сигнала, но и локализовать место выброса. Ясно, что с помощью преобразования Фурье подобную задачу решить не удастся.

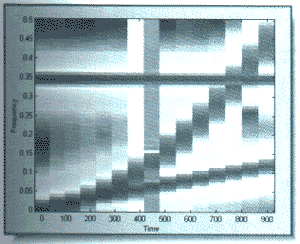
Рис. 7. Спектрограмма модифицированного сигнала (применяется окно Ханинга шириной 128 отсчетов). На экране уровни спектральных составляющих отображаются цветами

    При использовании кратковременного преобразования Фурье мы получим следующую картину.

    Смоделируем сигнал s₁ :

% загружает тестовый файл
mishmash.mat
load mishmash;
% моделируем выброс
mishmash(500)=3;
mish_delt=mishmash;
% создаем на диске файл,
содержащий модифицированный
сигнал
save mish_delt;
% отображаем на экране спектрограмму модифицированного
сигнала
specgram(mish_delt,128,1,128) ;

    С помощью спектрограммы (рис. 8) можно определить наличие выброса, но не удается точно локализовать его. Это связанно с принципом неопределенности, который гласит, что невозможно одновременно получить хорошее разрешение по частоте и по времени. Принцип неопределенности для преобразования Фурье может быть записан в виде

4 p D w * D t > 1.

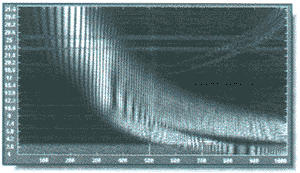
Рис. 8. Абсолютное значение wavelet-коэффициентов, полученных при анализе модифицированного сигнала с помощью wavelet Мейера

    Таким образом, если сигнал локализован во времени, то его спектр, напротив, рассредоточен по всей оси частот, и наоборот.

    Именно это свойство обуславливает основные ограничения применимости кратковременного преобразования Фурье. Wavelet-преобразование решает эту и некоторые другие проблемы. На рис. 9 можно не только определить наличие выброса, но и точно оценить его положение.

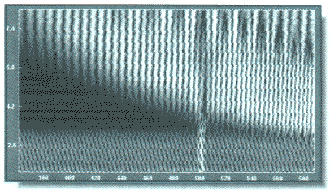
Рис. 9. Увеличенный участок рисунка 8

    В GUI также можно увеличить интересующий участок изображения. Для этого переместите выделяющий прямоугольник (держа нажатой левую клавишу мыши) в область сигнала, который требуется увеличить. Далее следует щелкнуть по кнопке "XY+" (расположенной внизу экрана), чтобы увеличить изображение по горизонтали и вертикали.

    Программа увеличит отображаемый сигнал и график коэффициентов. На увеличенном участке (рис. 10) можно удостовериться в наличии выброса и более точно определить его местоположение.

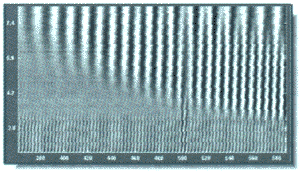
Рис. 10. Wavelet-коэффициенты, полученных при анализе модифицированного сигнала с помощью wavelet Мейера

    Можно изменить масштаб анализируемого сигнала и повторить анализ. Для этого следует отредактировать необходимые поля и снова нажать кнопку ЭAnalyzeЭ. Утилита позволяет выбирать: выводить сами wavelet-коэффициенты или их абсолютное значение.

    Для этого необходимо выбирать режим из меню ЭColoration mode", находящимся прямо над кнопкой "Analyze". При выводе самих wavelet-коэффициентов (рис. 11) цвета "масштабируются" между минимумом и максимумом значений коэффициентов. При выводе их абсолютных значений - цвета "масштабируются" между нулем и максимальным значением коэффициентов.

Заключение

    В заключении следует отметить, что GUI Wavemenu является удобным инструментом для предварительного анализа сигналов с помощью wavelet-преобразования. Он имеет дружественный интерфейс, и с его помощью можно использовать практически все возможности тулбокса Wavelet.

    Инструмент GUI полезен и в учебном процессе. С эго помощью можно демонстрировать многие важные свойства и возможности wavelet-преобразований.

    Авторы считают своим долгом выразить благодарность фирме "SoftLine" (http://www.softline.ru) за предоставленное программное обеспечение.

Литература

1. Strang G., Nguyen T. Wavelets and Filters Banks. - Wellesley-Cambridge-Press 1996. - 490 p.
2. Daubechies Ingr id, Ten lectures on wavelets, SIAM, Philadelphia, 1992.
3. Петухов А.П. Введение в теорию базисов всплесков. - СПб.: Изд-во СПбГТУ. - 1999. - 132 с.
4. Michel Misiti, Yves Misiti, Georges Oppenheim, Jean-Michel Poggi. Wavelet Toolbox for use with Matlab (User's Guide, version 1). - 626 p.
5. Потемкин В.Г. MATLAB 5 для студентов /Диалог-МИФИ. - 1999. - 447 с.

E-mail: arturlan@robotek.ru